自动机理论:术语及其应用
在当今的技术时代,硬件和软件领域都有了巨大的发展。硬件设计方法是开发的主要领域之一。随着技术的发展,硬件的概念。。。
在当今的技术时代,硬件和软件领域都有了巨大的发展。硬件设计方法是开发的主要领域之一。随着技术的发展,软硬件协同设计的概念得以实现。通过开发不同的方法,使用软件可以对硬件系统进行全面的设计和模拟。其中一种方法是自动机理论。自动机理论是计算机科学的一个分支,它涉及设计自动遵循预定步骤序列的计算设备的抽象模型。本文讨论了自动机教程的简要信息。
什么是自动机理论?
Automata一词源自希腊语,意思是“自我行动”。自动机是机器的数学模型。自动机由状态和转换组成。当输入被提供给自动机时,它会根据转换函数转换到下一个状态。转换函数的输入是当前状态和最近的符号。如果自动机有有限个状态,它被称为有限自动机或有限状态机。有限自动机由5元组(Q,∑,δ,qo,F)表示
哪里
Q=状态的有限集合。
∑=符号的有限集合,也称为自动机的字母表。
δ=过渡函数。
qo=输入的初始状态。
F=Q的最终状态集。
自动机理论的基本术语
自动机理论的一些基本术语是-
1..字母表:自动机理论中的任何有限符号集都被称为字母表。由字母∑表示的集合{a,b,c,d,e,}称为字母集,而集合“a”、“b”、“c”、“d”、“e”的字母称为符号。
2..一串:在自动机中,字符串是取自字母集∑的有限符号序列。例如,字符串S=“adeaddadc”在字母集∑={a,b,c,d,e,}上有效。
3..字符串长度:字符串中存在的符号数称为字符串长度。对于字符串S=“adaada”,字符串的长度为|S |=6。如果字符串的长度是0,那么它被称为空字符串。
4..克莱恩星:它是符号集∑上的一元运算符,它给出了集∑上所有可能长度的所有可能字符串的无限集,包括λ。它由表示。例如,对于集合∑={c,d},∑*={λ,c,d,cd,dc,cc,dd,……}。
5..克莱恩闭合:它是字母表集合中除λ之外的所有可能字符串的无限集合。它表示为。对于集合∑={a,d},∑+={a、d、ad、da、aa、dd,….}。
6..语言:语言是一些字母集∑的Kleene星集∑*的子集。语言可以是有限的,也可以是无限的。例如,如果一种语言在集合∑={a,d}上取所有长度为2的可能字符串,则L={aa,ad,da,dd}。
形式语言与自动机
在自动机理论中,形式语言是一组字符串,其中每个字符串由属于有限字母集∑的符号组成。让我们考虑一种cat语言,它可以包含下面无限集合中的任何字符串…
喵!
呜呜!
哇!!……
猫语言的字母集是∑={m,e,w,!}。让这个集合用于有限状态自动机模型-m。然后,以模型m为特征的形式语言表示为
L(米)
L(m)={‘新!’,‘新!”,‘新世界’,……}
自动机对于定义一种语言很有用,因为它可以以封闭的形式表达无限集。形式语言与我们日常生活中所说的自然语言不同。与我们的常规语言不同,形式语言可以表示机器的不同状态。形式语言用于对自然语言的一部分进行建模,如语法等。形式语言是由有限状态自动机定义的。有限状态自动机有两个主要的视角——可以判断字符串是否在该语言中的接受者,第二个视角是只产生该语言中字符串的生成器。
确定的有穷自动机
在确定性自动机中,当给出输入时,我们总是可以确定转换到哪个状态。因为这是一个有限自动机,所以它被称为确定性有限自动机。
图形表示法
状态图是用于确定性有限自动机的图形表示的有向图。让我们通过一个例子来理解。设确定性有限自动机为…
Q={a,b,c,d}。
Σ = {0, 1}
={a}
F={d}并且转换函数为
状态图
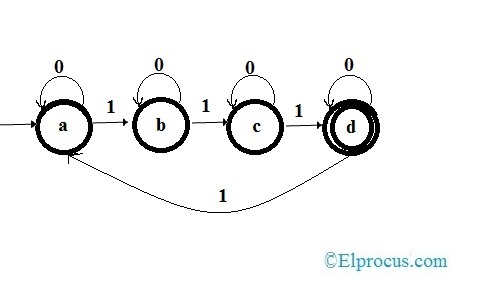
确定性有限状态自动机的状态图
从状态图
- 状态由顶点表示。
- 转换由标有输入字母表的圆弧表示。
- 空的单个传入弧表示初始状态。
- 带有双圆的状态是最终状态。
非确定性有限自动机
不能确定给定输入的输出状态的自动机称为非确定性自动机。它也被称为非确定性有限自动机,因为它有有限数量的状态。非确定性有限自动机表示为5元组的集合,其中(Q,∑,δ,qo,F)
问=状态的有限集合。
∑=字母表集合。
δ=转换函数
哪里:![]() 质量保证=初始状态。
质量保证=初始状态。
图形表示法
借助状态图来表示非确定性有限自动机。设非确定性有限自动机为-
Q={a,b,c,d}
Σ = {0,1}
qo={a}
F={d}
过渡是

状态图
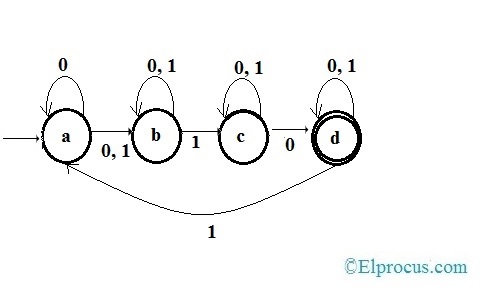
自动机理论的应用
自动机理论的应用包括以下几个方面。
- 自动机理论在计算理论、编译器生成、人工智能等领域非常有用。
- 对于文本处理编译器和硬件设计来说,有限自动机发挥着重要作用。
- 对于人工智能和编程语言中的应用程序,上下文无关语法非常有用。
- 在生物学领域,细胞自动机是有用的。
- 在有限域理论中,我们也可以找到自动机的应用。
在本文中,我们简要介绍了自动机理论语言和计算。自动机从史前时期就已经存在了。随着新技术的发明,这个领域出现了许多新的发展。你遇到过哪种类型的自动机?
