什么是谐振子：框图及其类型

简谐运动是由法国数学家让-巴蒂斯特·约瑟夫·傅立叶男爵于1822年发明的。Edwin Armstrong（1890年12月18日至1954年2月1日）在1992年的实验中观察到了振荡，Alexander Meissner（1883年9月14日至1958年1月3日）在1993年3月发明了振荡器。谐波是一个拉丁词。本文概述了谐振子的定义、类型及其应用。

什么是谐波振荡器？

谐振子被定义为一种运动，其中力与来自平衡点的粒子成正比，并产生正弦波形的输出。引起谐波运动的力在数学上可以表示为

F=-Kx

哪里

F=恢复力

K=弹簧常数

X=距平衡点的距离

ding="async" class="size-full wp-image-37257" src="https://uploads.9icnet.com/images/aritcle/20230518/blockdiagram-of-harmonic-oscillator.jpg" alt="block-diagram-of-harmonic-oscillator" width="428" height="212" sizes="(max-width: 428px) 100vw, 428px">

在谐波运动中有一个点，系统在其中振荡，而将质量一次又一次地带到它开始的同一点的力，该力被称为恢复力，该点被称为平衡点或平均位置。这种振荡器也被称为线性谐振子能量从振荡器中的有源部件流到无源部件。

方框图

这个谐振子的方框图由放大器和反馈网络组成。放大器用于放大信号，放大后的信号通过反馈网络并产生输出。其中Vi是输入电压，Vo是输出电压，Vf是反馈电压。

实例

弹簧上的质量：弹簧提供加速质量的恢复力，恢复力表示为

F=马

其中“m”是质量，a是加速度。

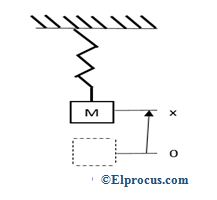
弹簧由质量（m）和力（F）组成。当力在点x=0拉动质量时，仅取决于质量的x位置，弹簧常数由字母k表示。

谐振子的类型

这种振荡器的类型主要包括以下几种。

强迫谐波振荡器

当我们对系统的运动施加外力时，运动就被称为强迫谐振子。

阻尼谐波振荡器

这个振子被定义为，当我们向系统施加外力时，振子的运动减少，它的运动被称为阻尼谐波运动。阻尼谐振子有三种类型，它们是

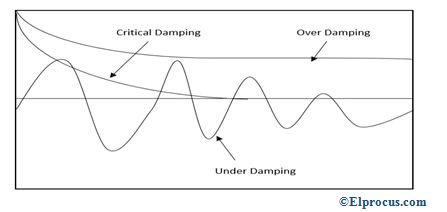
过阻尼

当系统缓慢地向平衡点移动时，则称其为过阻尼谐振子。

次阻尼

当系统迅速向平衡点移动时，就称其为过阻尼谐振子。

临界阻尼

当系统在不绕平衡点振荡的情况下尽可能快地移动时，则称其为过阻尼谐振子。

量子

它是由哥廷根大学的Max Born、Werner Heisenberg和Wolfgang Pauli发明的。量子这个词是拉丁语，量子的意思是少量的能量。

零点能量

零点能量也被称为基态能量。它被定义为基态能量总是大于零，这一概念是由德国的马克斯·普朗克和1990年开发的公式发现的。

阻尼简谐振子方程的平均能量

有两种类型的能量，它们是动能和势能。动能和势能之和等于总能量。

E=K+U………………。等式（1）

式中E=总能量

K=动能

U=势能

其中k=k=1/2 mv^2.…………当量（2）

U=1/2 kx^2.…………当量（3）

每个振荡周期的动能和势能的平均值等于

哪里v^2.=宽^2.（A）^2.-x^2.) ……. 方程（4）

将等式（2）和等式（3）中的等式（4）代入，将得到

k=1/2米[w^2.（A）^2.-x^2.)]

=1/2米[Aw cos（重量+ø<sub>0)]^2.……. 方程（5）

U=1/2 kx^2.

=1/2 k[A sin（wt+ø₀)]^2.……. 方程（6）

将方程（1）中的方程（5）和方程（6）代入，得到总能量值

E=1/2米[w^2.（A）^2.-x^2.)]+1/2千倍^2.

=1/2米宽^2.-1/2米宽^2.A.^2.+1/2千倍^2.

                =1/2米宽^2.A.^2.+1/2 x^2.（千兆瓦^2.)……. 方程（7）

哪里兆瓦^2.=K，将该值代入等式（7）

            E=1/2千A^2.-1/2 Kx^2.+1/2 x^2.=1/2千年^2.

总能量（E） =1/2千年^2.

一个时间段的平均能量表示为

K_平均值=单位_平均值=1/2（1/2千A^2.)

谐振子波函数

哈密顿算符表示为动能和势能的和，它表示为

（Q）=T+V…………..等式（1）

式中？=哈密尔顿算子

T=动能

V=势能

要生成波函数，我们必须知道薛定谔方程，方程表示为

-ђ^2./2μ*天^2.ѱ_υ（Q） /天Q^2.+1/2千克^2.ѱ_υ（Q） =电子_υѱ_υ（Q） …………。方程（2）

其中Q=法线坐标的长度

Μ=有效质量

K=力常数

薛定谔方程的边界条件为：

Ѱ(-∞) = ø

Ѱ(+∞) = 0

我们也可以将等式（2）写成

    d^2.ѱ_υ（Q） /天Q^2.+ 2μ/ђ^2.（E）_υ-K/2*Q^2.) ѱ_υ（Q） =0…………..当量（3）

用于求解方程的参数为

β=？/√μk………。。方程（4）

d^2./dQ值^2.= 1/β^2.d^2./dx公司^2.………….. 方程（5）

将等式（4）和等式（5）代入等式（3），则该振荡器的微分方程变为

d^2.ѱ_υ（Q） /dx^2.+ (2μβ^2.E_υ/ ђ^2.–x^2.) ѱ_υ（x） =0………。。方程（6）

幂级数的一般表达式为

∑C－nx2…………。方程（7）

指数函数表示为

exp（-x^2./2） …………当量（8）

等式（7）乘以等式（8）

ѱυ（x）=∑C？nx2exp（-x2/2）……………。。方程（9）

埃尔米特多项式是通过使用以下方程获得的

ђ_υ^­­­（x） =（-1）^υ*经验（x^2.)d/dx^υ*exp（-x^2.) …………….. 方程式（10）

归一化常数表示为

                                             N_υ= (1/2^υυ!√Π)^1/2…………..当量（11）

这个单谐振子解决方案表示为

Ѱ_υ（x） =N个_υH_υ（y） 电子^-x2/2个…………..当量（12）

其中N_υ是归一化常数

H_υ­­­是隐士吗

e^-2个/2.是高斯

方程（12）是谐波振荡器的波函数。

该表显示了最低能量状态的第一项埃尔米特多项式

υ	0	1.	2.	3.
Hυ（y）	1.	第2年	第4年2.-2	8年3.-12年

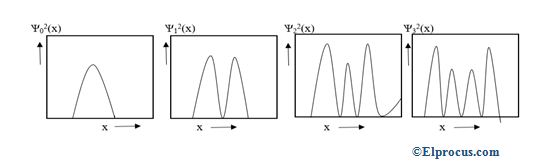
的波函数简谐振子图对于四种最低能量状态，如下图所示。

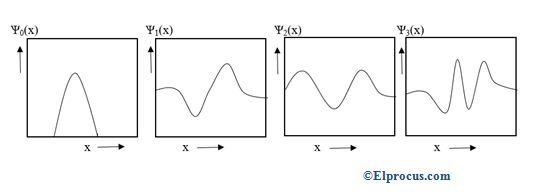
该振荡器在四种最低能量状态下的概率密度如下图所示。

应用

年代单谐振荡器应用程序主要包括以下内容

• 音频和视频系统
• 无线电和其他通信设备
• 逆变器、警报
• 蜂鸣器
• 装饰灯

优势

这个谐振子的优点是

• 花钱少的
• 高频发电
• 高效率
• 花钱少的
• 便携式的
• 经济的

示例

此振荡器的示例包括以下内容。

• 乐器
• 单摆
• 质量弹簧系统
• 摆动
• 时钟指针的运动
• 汽车、卡车、公共汽车等车轮的运动

这是一种我们可以在日常基础上观察到的运动。利用薛定谔导出了谐振子的波函数和谐振子的方程。这里有一个问题，蹦极是做什么动作的？