在任何电气和电子电路中，电源用于向负载提供电能，无论负载在何处变为功能工作。基本上，由于加热效应以及电路内的其他限制，整个电源不会有负载。因此，在获取权力和传递权力之间存在一定的区别。负载的大小将影响从电源输送的功率的总和，负载电阻内的任何变化都可能导致向负载的功率传输内的变化。因此，最大功率传输定理或MPTT确保了向负载输送最大功率的条件。


在任何电子或电气应用中，通过负载获得的功率之和都是一个重要参数。例如，直流电路中的负载可以通过电阻为“RL”欧姆的晶体管来表示。在交流电路中，我们可以通过阻抗为“ZL”欧姆的复杂负载来指示它。本文讨论了MPPT（最大功率转移定理）的概述。

什么是最大功率转移定理？

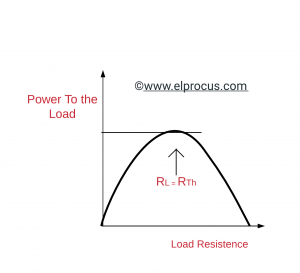
这个最大功率转移定理可以定义为，当负载电阻（R<sub>L)等效于内阻，那么它接收的最高功率被称为源网络的Thevenin等效电阻。该定理定义了当源电阻给定一次时如何选择负载电阻（RL）。在相反的情况下应用该定理是一个普遍的误解。

这并不意味着如何选择特定负载电阻（RL）的源电阻。事实上，除了负载电阻的值之外，最大限度地利用功率传输的源电阻始终为零。该定理可以扩展到包括电抗的AC电路，并定义当负载阻抗（ZL）必须等于ZTH（相应电路阻抗的复共轭）时，发生最高功率传输。

ding="async" class="wp-image-35046 size-large" src="https://uploads.9icnet.com/images/aritcle/20230518/Maximum-Power-Transfer-Theorem-1024x547.png" alt="Maximum Power Transfer Theorem" width="850" height="454" sizes="(max-width: 850px) 100vw, 850px">
最大功率转移定理

最大功率转移定理已解决的问题

1). 找到使电路（端子a和b的左侧）能够向负载输送最大功率的负载电阻RL。此外，还要找到输送到负载的最大功率。

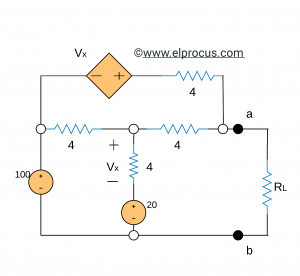
Maximum Power Transfer Theorem Example
最大功率转移定理示例

解决方案：

为了应用最大功率转移定理，我们需要找到Thevenin的等效电路。

（a） 电路的Vth导数：开路电压

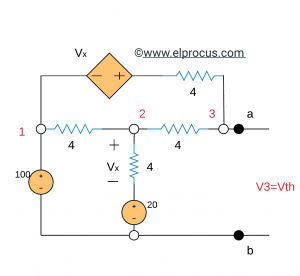
open-circuit voltage
开路电压

限制条件：V1=100，V2–20=Vx，V3=Vth

在节点2：

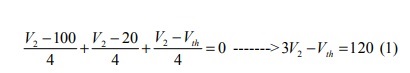
在节点3处：

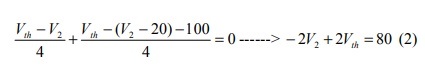
（1） *2+（2）*3–>Vth=120[V]

（b） Rth推导（通过测试电压法）：在停用和施加测试电压后，我们有：

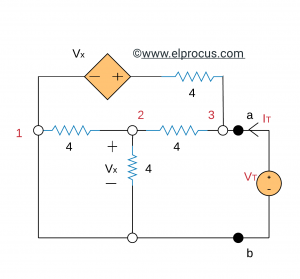
After deactivation & test voltage application
停用和测试电压施加后

限制条件：V3=VT和V2=Vx

在节点2：

在节点3（KCL）：

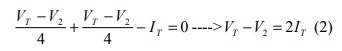
根据（1）和（2）：

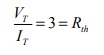
（c） 最大功率传输：现在电路减少到：

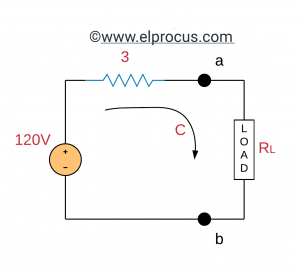
Result Circuit
结果电路

为了获得最大功率传输，则RL＝3＝Rth。最后，传输到RL的最大功率为：

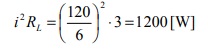
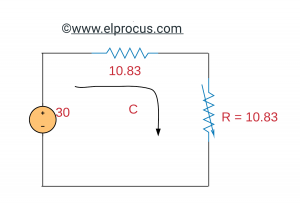
2). 确定可输送至可变电阻器R的最大功率。

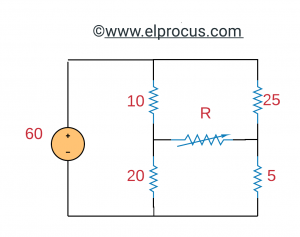
Maximum Power Transfer Theorem Example 2
最大功率转移定理示例2

解决方案：

（a） Vth：开路电压

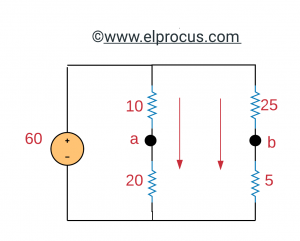
Vth_ Open circuit voltage
Vth_开路电压

从电路来看，Vab=Vth=40-10=30[V]

（b） Rth：让我们应用输入电阻法：

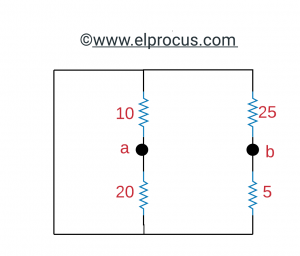
Rth_ Let’s apply Input Resistance Method
Rth让我们应用输入电阻法

然后Rab=（10//20）+（25//5）=6.67+4.16=10.83=Rth。

（c） Thevenin电路：

Thevenin circuit
戴维南电路

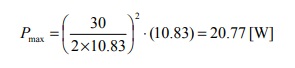
MPTT公式

这个最大功率转移定理公式将在下面进行解释。如果我们将η（效率）视为通过负载溶解的功率的分数R以与源一起扩展功率，虚拟电视，那么计算最大功率传输效率像

η=（Pmax/P）X 100=50%

哪里最大功率（Pmax）

P最大值=V2.真实航向R第(R第+R真实航向)2=五、2.第/4小时真实航向

并且所提供的功率（P）为

P=2伏2.第/4小时真实航向=伏2.真实航向/2小时真实航向

当达到最高功率转移时，η仅为50%，尽管当R达到100%时L（负载电阻）达到无穷大，而整个功率级趋于零。

交流电路的最大功率转移定理

在交流电路中，MPTT提供阻抗条件，以向负载传输最高功率。该定理指出，在有源交流电路中，包括通过内部阻抗的电源，如ZS，该电源连接到负载，如ZL。因此，一旦负载阻抗等于ZS或源阻抗的复合共轭，最大功率转移主要发生在源到负载之间。

作为非活动布置，最高功率被传输到负载，而负载的阻抗等效于从负载的端子观察到的给定设置的相应阻抗的复共轭。

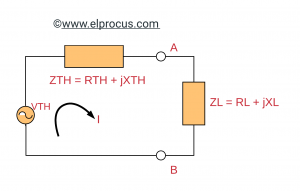
Maximum Power Transfer Theorem For A.C Circuits
交流电路的最大功率转移定理

上述电路与Thevenin的电路等效。当考虑负载端子之间的上述电路时，电流将如下所示

I=VTH/ZTH+ZL

式中ZL=RL+jXL

ZTH=RTH+jXTH

因此

I=VTH/（RL+jXL+RTH+jXTH）

=VTH/（（RL+RTH）+j（XL+XTH））

循环到负载的功率，

PL=I2 RL

PL=V2TH×RL/（（RL+RTH）2+（XL+XTH）2）……（1）

对于最高功率，上述方程的导数应该为零，在简化之后，我们可以得到以下结果。

XL+XTH=0

XL=–第x个

将上述等式1中的XL值代入，然后我们可以得到以下结果。

PL=V2TH×RL/（（RL+RTH）2

同样，对于最高功率传输，上述方程的推导必须等于零，求解后我们可以得到

RL+RTH=2 RL

RL=第

因此，如果交流电路中RL（负载电阻器）=RTH&XL=–XTH，则最高功率将从电源传输到负载。这意味着负载阻抗（ZL）必须等于ZTH（相应电路阻抗的复共轭）

ZL=第z个

该最大发射功率（Pmax）=V2TH/4 RL或V2TH/4 RTH

直流电路的最大功率转移定理

MPTT用于直流电路，它定义了从有源网络到外部负载电阻的最高功率传输的声明。它定义了在有源、线性、双向直流n/w中，一旦外部负载电阻等于电源的内阻，最高功率将从电源输送到电负载。

MPTT的开发可以通过参考电压源或实际电流来完成。如果电源是独立的电压源或实用的，则其内部串联电阻应等于负载电阻，以传输最高功率。

独立的电流源或实用的并联内阻必须等于负载电阻。直流电路中的内部电源串联电阻改变了传输到负载的功率，因此从电源向电负载传输的最高电流受到限制。

MPTT证明

这个最大功率转移定理的证明在某些应用中，电路的目的是为负载提供最大功率。一些例子：

  • 立体声放大器
  • 无线电发射器
  • 通信设备

如果整个电路被其Thevenin等效电路取代，则负载除外，如下所示，负载吸收的功率为：

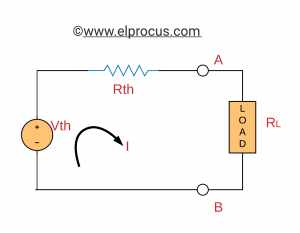
Maximum Power Transfer Theorem Proof
最大功率转移定理的证明

PL=我2.RL=（V第/对第+对L)2.x右L=伏2.第RL/（R）第+对L)2.

由于给定电路的VTH和RTH是固定的，因此负载功率是负载电阻RL的函数。

通过对PL相对于RL进行微分并将结果设为零，我们得到了以下最大功率转移定理；当RL等于RTH时，出现最大功率。

当满足最大功率传输条件时，即RL=RTH，传输的最大功率为：

Differentiating PL with respect to RL
相对于RL区分损益

PL=伏2.第RL/[R]第+对L]2.=伏2.第R第/[R]第+对L]2.=伏2.第/4小时第

利用最大功率传递定理求解网络的步骤

以下步骤用于通过最大功率转移定理解决问题

步骤1：拆除电路的负载电阻。

第2步：通过开路负载端子查找源网络的戴维南电阻（RTH）。

步骤3：根据最大功率传输定理，RTH是网络的负载电阻，即RL=允许最大功率传输的RTH。

步骤4：最大功率传输通过以下公式计算

（Pmax）=V2TH/4 RTH

最大功率转移定理示例问题及其解

找到功率最高的以下电路的RL值，使用最大功率转移定理通过RL找到最高功率。

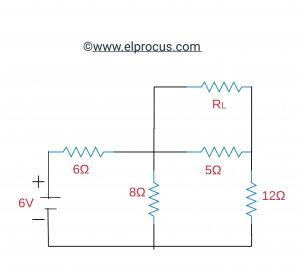
Finding RL value
查找RL值

解决方案：

根据这个定理，当通过负载的功率最高时，电阻类似于消除RL后RL两端之间的相等电阻。

因此，对于负载电阻（RL）的发现，我们必须发现等效电阻：

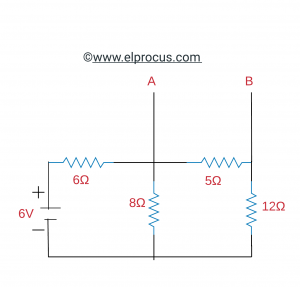
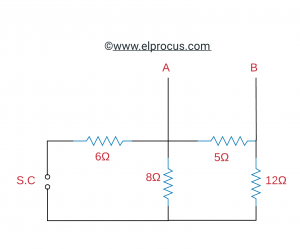
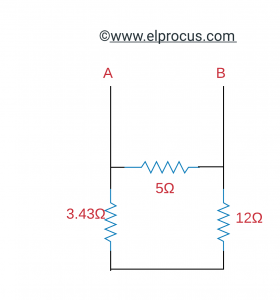
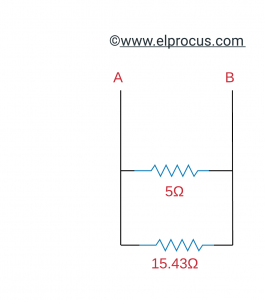
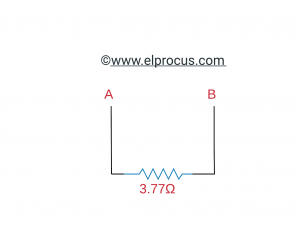
所以

现在，为了通过RL负载电阻发现最高功率，我们必须发现VOC电路之间的电压值。

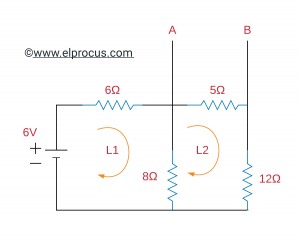
对于上述电路，应用网格分析。我们可以获得：

对回路1应用KVL：

6-6I1-8I1+8I2=0

-14I1+8I2=-6（1）

对回路2应用KVL：

-8I2-5I2-12I2+8I1=0

8I1-25I2=0（2）

通过求解上述两个方程，我们得到

I1=0.524 A

I2=0.167 A

现在，从电路Vo.c是

VA-5I2-VB=0

Vo.c/VAB=5I2=5X0.167=0.835v

因此，通过负载电阻（RL）的最大功率为；

P最大值=V有机碳2./4小时L=（0.835 x 0.835）/4 x 3.77=0.046瓦

发现可以传输到以下电路的RL负载电阻器的最高功率。

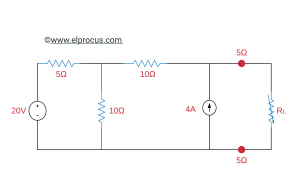
Maximum Power to RL
RL的最大功率

解决方案

将Thevenin定理应用于上述电路，

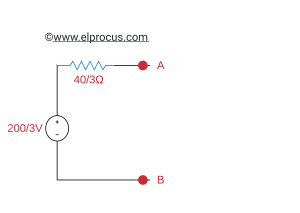
这里，Thevenin的电压（Vth）=（200/3），Thevenen的电阻（Rth）＝（40/3）Ω

用Thevenin等效电路代替电路的分数，即给定电路的端子A和端子B的左侧。二次电路图如下所示。

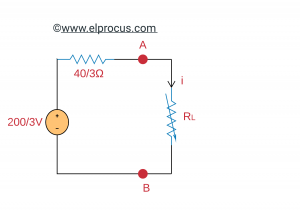
我们可以通过使用以下公式找到将输送到负载电阻器RL的最大功率。

PL，最大值=V2TH/4 RTH

将上式中的VTh=（200/3）V和RTh=（40/3）Ω代入。

PL，最大=（200/3）2./4（40/3）=250/3瓦

因此，将被输送到给定电路的负载电阻器RL的最大功率是250/3W。

优点和缺点

最大功率转移定理的优点和缺点包括以下几个方面。

  • 最大功率转移定理的主要优点是，它可以分析任何点的性能
  • 最大功率转移定理的主要缺点是，它不适用于非线性和单向网络。
  • 最大功率传递定理的局限性在于，由于其50%的效率，它不适用于电力系统。因此，主要关注的是效率。
  • 这个定理可以应用于通信线而不是电力线，因为如果我们应用于电力线，那么实际问题就会发生，如下所示。
  • 在电力线中，接收端电压恒定是一个重要条件，因此该定理忽略了这一特征。
  • 由于效率较低，这在电力线内是不能接受的。

最大功率转移定理的应用

最大功率转移定理可以以多种方式应用于确定从电源接收最大功率的负载电阻值以及在最高功率转移状态下的最大功率。以下是最大功率转移定理的一些应用：

  • 这个定理总是在通信系统中被寻求。例如，在社区地址系统中，通过使扬声器（负载电阻）等效于放大器（源电阻），电路被调谐为最高功率传输。当负载和电源匹配时，它具有相等的电阻。
  • 在汽车发动机中，传输到汽车电机启动器的功率将取决于电机的有效电阻和电池的内阻。当两个电阻相等时，最高功率将传输到电机以启动发动机。
  • 最大功率转移定理可以应用于复杂网络，如下所示
  • 它用于交流和直流网络。
  • 为了在公共广播系统中实现最大功率传输，可以通过使类似RL（负载电阻）的扬声器等效于类似放大器的源电阻来改变电路。一旦源和负载都包括等效电阻，那么它们就匹配了。
  • 这个定理适用于所有自主电压源被停用的地方&只需考虑相同的阻抗，就可以传输最大数量的功率。
  • 在无线电通信中，如果电路内的负载阻抗等于源的阻抗，则功率放大器向天线广播最高量的信号。
  • 在音频系统中，它被用于需要向扬声器传递信息的地方。一旦负载阻抗等于源阻抗，放大器就会改变最高的语音量。
  • 在电阻网络中，一旦负载电阻等于通过负载观察到的电阻，电阻负载就会提取最大功率，因为它会向后看网络。
    事实上，可以朝向网络输出端子访问电阻。事实上，如果我们把完整的网络看作电压源，这个电阻就是Thevenin定理中描述的Thevenin等效电阻。同样，如果我们将网络视为电流源，那么这个电阻将被称为诺顿等效电阻，可以在诺顿定理中描述。
  • 它被用于各种电路中，其中电路是基于效率原理设计的，效率原理将降低50%。然而，消费者在电力受到限制的地区使用这种MPTT，如移动接收器和音频扬声器。
  • 为了向网络中使用的负载输送最高功率，这种较低的效率是可以承受的。在电力系统中，发电机和输电系统内的电压降和功率损失都很小。
  • 这里，与电源的内部阻抗相比，负载阻抗高出数倍
  • 因此，电源电路在最佳匹配条件下工作。例如，在电力传输中，效率最高的地方很重要，所以我们设计基于最高电压的系统。但由于50%的损耗，不可能抵抗散热，因为输送的功率为100兆瓦。

这都是关于最大幂定理的。最后，根据上述信息，我们可以得出结论，这个定理经常被用来确保最高功率可以从电源传输到负载。这里有一个问题要问你，最大功率转移定理的优点是什么？