二极管主要是单向器件。当施加正向或正电压时，它提供低电阻，而当二极管反向偏置时，它具有高电阻。理想的二极管具有零正向电阻和零电压降。二极管提供高反向电阻，从而产生零反向电流。虽然不存在理想二极管，但在一些应用中使用了接近理想的二极管。电源电压通常比二极管的正向电压大得多，因此V<sub>F假定为常数。当负载电阻通常很高或很低时，使用数学模型来近似硅和锗二极管的特性。这些方法有助于解决现实世界中的问题。本文讨论了什么是二极管近似，近似的类型，问题和二极管近似模型。


什么是二极管？

二极管是一种简单的半导体，有两个称为阳极和阴极的端子。它允许电流在一个方向（正向）流动，并限制电流在相反方向（反向）流动。正向偏置时电阻较低或为零，反向偏置时电阻较高或无穷大。端子阳极指的是正极引线，阴极指的是负极引线。当阳极与正电压连接时，大多数二极管传导或允许电流流动。二极管被用作电源中的整流器。


ding="async" class=" wp-image-37918" src="https://uploads.9icnet.com/images/aritcle/20230518/diode.jpg" alt="Semiconductor-diode" width="277" height="202" sizes="(max-width: 277px) 100vw, 277px">


半导体二极管

什么是二极管近似？

二极管近似是一种数学方法，用于近似实际二极管的非线性行为，以便进行计算和电路分析。有三种不同的近似值用于分析二极管电路。


第一二极管近似

在第一近似方法中，二极管被认为是一个正向偏置的二极管，并且是一个电压降为零的闭合开关。它不适合在现实生活中使用，但仅用于不需要精确性的一般近似。


First-approximation


第一近似

第二二极管近似

在第二种近似中，二极管被认为是一个与电池串联的正向偏置二极管，以打开设备。硅二极管需要0.7V才能导通。0.7V或更高的电压被馈送以导通正向偏置的二极管。如果电压低于0.7V，二极管将熄灭。


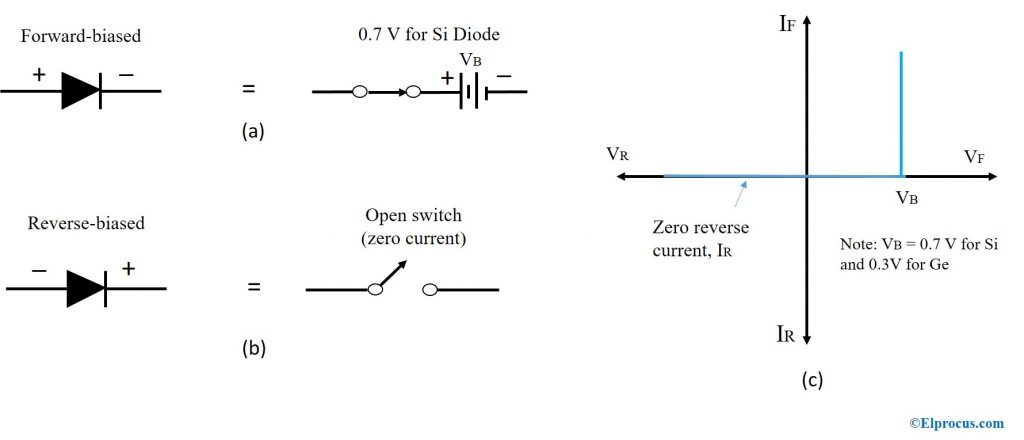
Second-approximation


二次近似

第三二极管近似

二极管的第三近似值包括二极管两端的电压和体电阻两端的电压RB体电阻较低，例如小于1欧姆并且总是小于10欧姆。体积电阻RB对应于p和n材料的电阻。该电阻基于在任何给定时间流过二极管的正向电压和电流的量而变化。


二极管两端的电压降使用以下公式计算


五、d=0.7伏+我d*对B


如果RB<1/100 RTh公司或RB<0.001 RTh公司，我们忽略了这一点


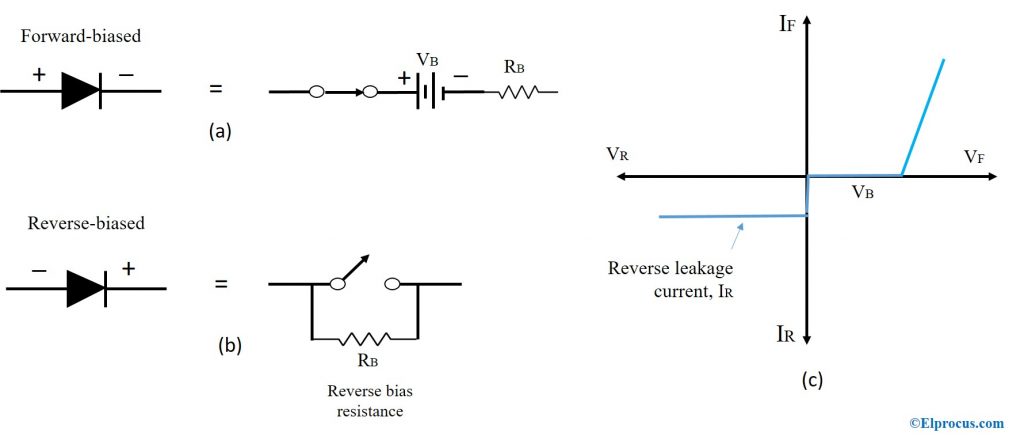
Third-approximation


第三近似

二极管近似问题及其解

现在让我们看看二极管近似问题的两个例子及其解决方案


1). 查看下面的电路，使用二极管的第二近似值，找到流经二极管的电流。


Circuit-for-diode-approximation


二极管近似电路

我D=（Vs–VD)/R=（4-0.7）/8=0.41A


2). 查看这两个电路，并使用二极管的第三近似方法进行计算


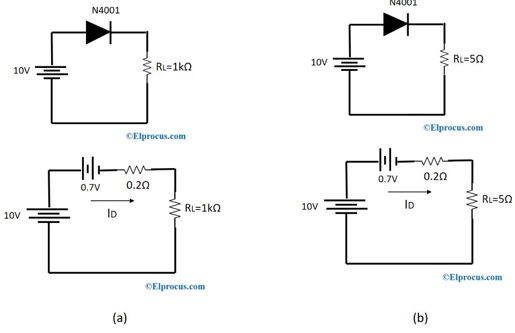
Circuits-using-third-method


使用第三种方法的电路

对于图（a）


将1kΩ电阻器与0.2Ω大容量电阻器相加不会对电流产生任何影响


我D=9.3/1000.2=0.0093 A


如果我们不计算0.2Ω，那么


我D=9.3/1000=0.0093 A


对于图（b）


对于5Ω的负载电阻，忽略0.2Ω的体电阻会导致电流差异。


因此，必须考虑体电阻，电流的正确值为1.7885 A。


我D=9.3/5.2=1.75885 A


如果我们不计算0.2Ω，那么


我D=9.3/5=1.86 A


总之，如果负载电阻很小，那么体积电阻就会起作用。然而，如果负载电阻非常高（范围为几千欧姆），则体电阻对电流没有影响。


二极管近似模型

二极管模型是用于近似二极管的实际行为的数学模型。我们将讨论使用各种技术在正向偏置方向上连接的p-n结的建模。


肖克利二极管模型

在肖克利二极管模型方程中，p-n结二极管的二极管电流I与二极管电压VD有关。假设VS>0.5V，ID远高于is，我们用以下公式表示二极管的VI特性


我D=我S（e）VD/ηVT–1）-（i）


利用基尔霍夫环路方程，我们得到以下方程


我D=（VS–VD/R） ----（ii）


假设二极管参数为，η为已知，而ID和IS为未知量。这些可以使用两种技术找到——图形分析和迭代分析


迭代分析

对于任何给定的一系列值，使用迭代分析方法来找到二极管电压VD相对于VS，使用计算机或计算器。方程（i）可以通过将其除以IS并加1来重新组织。


eVD/ηVT=I/IS+1


通过在方程的两边应用自然对数，可以去除指数。方程简化为


五、D/ηV值T=英寸（I/IS+1)


用（ii）代替（i），因为它满足基尔霍夫定律，并且方程简化为


  五、D/ηV值T=（ln（VS–VD)/里S) +1


或


  五、D=ηVTln（（VS–VD)/里S+1)


由于Vs的值是已知的，因此可以猜测VD，并且将该值放在方程的右侧，并且执行连续运算，可以找到VD的新值。一旦VD被发现，基尔霍夫定律就被用来寻找I。


图形化解决方案

通过在i-V曲线上绘制方程（i）和（ii），在两个图的交点处获得近似的图形解。图上的这个相交点满足方程（i）和（ii）。图上的直线表示负载线，图上的曲线表示二极管特性方程。


Graphical-solution-to-determine-the-operating-point


确定操作点的图形解决方案

分段线性模型

由于图形求解方法对复合电路来说非常复杂，因此使用了二极管建模的另一种方法，即分段线性建模。在这种方法中，函数被分解为多个线性段，并用作二极管近似特性曲线。


该图显示了使用两段分段线性模型近似的实际二极管的VI曲线。实际二极管分为三个串联元件：理想二极管、电压源和电阻器。在Q点绘制的二极管曲线的切线和这条线的斜率等于二极管在Q点的电阻的倒数。


Piecewise-linear-approximation


分段线性近似

数学理想化二极管

数学上理想化的二极管是指理想的二极管。在这种类型的理想二极管中，当二极管被反向偏置时，流动的电流等于零。理想二极管的特性是当施加正电压时在0V导通，电流将是无限大的，二极管的行为就像短路。给出了理想二极管的特性曲线。


I-V-Characteristic-Curve


I-V特性曲线

常见问题解答

1). 哪种二极管模型代表了最准确的近似值？


第三种近似是最精确的近似，因为它包括0.7V的二极管电压、二极管内部体电阻两端的电压以及二极管提供的反向电阻。


2). 二极管的击穿电压是多少？


二极管的击穿电压是为使二极管击穿并沿相反方向导通而施加的最小反向电压。


3). 你如何测试二极管？


要测试二极管，请使用数字万用表


  • 将万用表选择开关切换到二极管检查模式

  • 将阳极连接到万用表的正极引线，将阴极连接到负极引线

  • 万用表显示的电压读数在0.6V到0.7V之间，并且知道二极管正在工作

  • 现在将万用表的接线反向

  • 如果万用表显示电阻无穷大（超出范围）并且知道二极管在工作

4). 二极管是电流吗？


二极管既不是电流控制的器件，也不是电压控制的器件。如果正电压和负电压给定正确，它将导通。


本文讨论了三种二极管近似方法。我们讨论了当二极管充当开关时，如何近似二极管，而开关的数值很少。最后，我们讨论了各种类型的近似二极管模型。这里有一个问题要问你，二极管的功能是什么？