什么是卡诺图及其示例
前面我们已经讨论了如何通过布尔公设和定理来简化布尔函数。但这个过程很耗时,而且在每一步之后,我们都必须重新表述简化的表达式。所以,卡诺地图介绍了。。。
前面我们已经讨论了如何通过布尔公设和定理来简化布尔函数。但这个过程很耗时,而且在每一步之后,我们都必须重新表述简化的表达式。因此,Karnaugh Map引入了一种通过简单地简化布尔函数来克服这一困难的方法。这种方法被称为卡诺图或K-map方法。这是一种图形化方法,包括2n个单元格用于“n”个变量。在单个比特位置中简单地改变连续的单元。例如,在一些数字电路和实际问题中,使用最小变量来找出表达式。在不使用任何布尔代数定理的情况下,使用卡诺图方法可以将布尔表达式简化为3到4个变量。基于这个问题,k-map使用了两种形式,如SOP——乘积和和和POS——乘积和。与真值表相比,k-map提供了更多的数据。本文讨论了卡诺图求解实例.
什么是卡诺图/K-Map?
卡诺图或K-Map是一种用于以系统的方式简化布尔表达式的方法。这种方法非常有助于找到乘积的最简单和和表达式的乘积,即最小表达式。为了简化起见,卡诺地图提供了一本食谱。
与真值表类似,卡诺图包括输入变量的所有可实现值及其等效输出值。但是,在卡诺图中,所有值都将存储在数组单元中。因此,在每个单元格中,每个输入的二进制值变量都可以存储。卡诺图方法主要用于包含2到5个变量的表达式。对于大量变量,使用Quine McClusky技术进行简化。
在卡诺图中,单元格的数量与可变输入排列的总数有关。例如,如果变量是三个,那么单元的数量是23=8。类似地,如果变量的数量是4,那么单元的数量是24=16。K-map使用两种形式,如SOP和POS。K-map网络由1和0填充。卡诺图可以通过分组来求解。
如何使用卡诺地图?
使用K-map求解表达式有不同的步骤。因此,根据可用的变量,选择卡诺图。以下列表是卡诺地图规则。
- 识别最小项,否则识别问题中显示的最大项。
- 对于乘积的和,将1放在k映射块中,对应于minterms,就像将0放在另一个地方一样)。
- 对于和的乘积,将0放在k映射块中,对应于最大项,比如在另一个地方放1)。
- 创建矩形组,其中包括除1之外的2、4或8次方的整个术语,并尽量在一个组中掩盖几个元素。
- 在形成组之后,产品术语需要找到并将它们相加,以获得产品总和的形式。
变量的卡诺映射
卡诺图方法主要用于减少2到5个变量的布尔函数。让我们逐一讨论2、3、4和5个变量的卡诺图
2个变量的K-Map
在这种类型的K放大器中,所使用的单元数量是4,因为变量的数量是2,那么单元的数量将是2n。因此,下图是2个变量的K映射,如下所示。
只有一个选项可以为4个连续的minterm进行分组。因此,对2个连续的minterm进行分组的可实现组合类似于(m0,m1)、(m2,m3)、(m0、m2)和(m1,m3)。
2个变量K映射的示例
通过使用K-map,我们可以简化以下两个变量的布尔表达式。
F=A B’+A’B+A‘B’
对于上述方程,真值表如下所示。
| A. |
B | F |
| 0 |
0 | 0 |
| 0 |
1. | 1. |
| 1. |
0 | 1. |
| 1. |
1. | 1. |
我们将“1”放在方程中提供的输出项处。
在上述2个变量的卡诺图中,可以根据规则形成两个组。第一条规则是将(A',B)和(A'、B')这两个术语组合在一起,第二条规则是组合(A,B')和(A',B'。
在这两组中,可以使用较小的右侧单元格。一旦变量分组完成,接下来的步骤就是确定最小化的表达式。通过从A’和B’这样的两组中删除频繁项,我们可以得到一个简化表达式的组合。所以最小化的方程将是X'+Y'。
三个变量的K-Map
在3个变量的K-map中,单元的数量是8,因为变量的数量是n=3,所以单元将变成2n=8。因此,3个变量的K映射图如下所示。
对于制作8个相邻的薄荷糖,只有一种可能性
用于对四个连续的minterm进行分组的可实现组合类似于(m0,m1,m3,m2)、(m0、m1、m4、m5)、(m4,m5,m7,m6)、(m1,m3、m5、m7)、(m2,m0,m6,m4)和(m3,m2,m7、m6)。
用于对两个连续的最小项进行分组的可实现的组合是{(m0,m1)、(m3,m2)、(m1,m3)、(m2,m0)、(m5,m7)、(m4,m5)、(m7,m6)、(m0,m4)、[m6,m4]、[m1,m5]和[m2,m6]和[m3,m7]}。
如果X=0,那么三个变量的K-map将变为两个变量的K-map。
3个变量K映射的示例
通过使用K-map,我们可以简化以下三个变量的布尔表达式。
F=A’B C+A’B’C+A B C’+A‘B’C’+ABC+AB’C’
对于上面的方程,首先,我们必须制作真值表
| A. | B | C | F |
| 0 |
0 | 0 | 1. |
| 0 |
0 | 1. | 1. |
| 0 | 1. | 0 | 0 |
| 0 |
1. | 1. | 1. |
| 1. |
0 | 0 | 1. |
| 1. | 0 | 1. | 1. |
| 1. |
1. | 0 | 1. |
| 1. | 1. | 1. | 0 |
我们将‘11’放在方程中提供的o/p项处。
在三变量卡诺图中,有8个细胞看起来如下。
在这个k映射中,我们将最左边的列视为最右边列的连续列。因此,可以像下面这样形成4个尺寸的组。
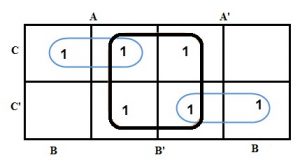
在这两方面,我们都有“B”的共同点。因此,4个大小的组可以像连词B一样减少。为了使用其中包含“1”的每个单元格,我们将剩余的单元格组合成2个大小组,如下所示。
这个组不包括常见的变量,因此它们是由它们的变量和它们的共轭来写的。因此,减少的方程将是AB’+B’+A’B,在这个方程中,无法实现进一步的减少。
4个变量的K-Map
对于4个变量的卡诺图,细胞的数量是16,因为变量的数量是4。因此,下面显示了4个变量的K映射图。
只有一个机会可以将16个连续的小学期分组。
设所有行的minterm可以相应地用R1、R2、R3和R4来表示。同样,所有列的minterm可以相应地用C1、C2、C3和C4表示。对8个连续的minterm进行分组的可实现组合是{(R1,R2)、(R3,R4)、(R4,R1)、(R2,R3)、(C1,C2)、(C3,C4)、(C2,C3)、(C4,C1)}。
如果A=0,那么4个变量的K-map将变为3个变量的K-map。
4个变量K映射的示例
通过使用卡诺映射,简化以下4个变量的布尔方程
F(X,Y,Z,W)=(1,5,12,13)
通过形成一个k映射,我们可以像下面这样减少所提供的布尔方程。
F=X Z’W+X’Z’W
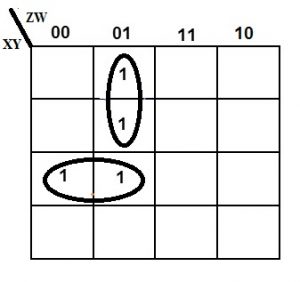
5个变量的K-Map
对于5个变量K-map,单元格的数量是32,因为变量的数量是5。因此,5个变量的K映射图如下所示。
只有一次机会将32个连续的小学期分组。因此,对16个连续的minterms进行分组的可能性有两种,类似于对m0到m15 minterms和m16到m31进行分组。
如果V=0,则5个变量的K-map将变为4个变量的K-map
在上述所有K映射中,使用了minterms表示法。同样,您可以使用最大术语表示法。
5个变量K映射的示例
使用k映射简化给定的5变量布尔方程。
f(X,Y,Z,W,A)=∑m(0,5,6,8,9,10,11,16,20,42,25,26,27)
通过形成k映射,我们可以简化所提供的布尔方程。
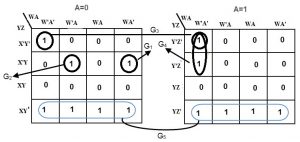
卡诺图与不在乎的条件
在卡诺图中,“不在乎”条件主要用于替换空白单元格,以计算出可实现的变量分组,该变量分组可以用作1或0,具体取决于组中的连续变量。
具有“不在乎”条件的单元格通过标准0和1之间的星号(*)表示。在变量分组中,可以忽略“不在乎”。这些条件对大变量的分组非常有帮助。
通过“不在乎”减少表情
我们可以通过将“不在乎条件”的相对函数赋值为1或0来定位它们,从而减少布尔表达式。在布尔方程中,如果不在乎的数量是“n”,那么获得的函数数量将是2n。
因此,这一切都是关于卡诺图或k-图方法的概述。这种方法更有助于减少包括变量数量的布尔表达式,如具有2个变量、3个变量、4个变量、5个变量的布尔表达式。这里有一个问题要问你,卡诺图的应用是什么。
