什么是二进制乘法器:工作原理及其应用
在数字系统中,诸如二进制乘法器、二进制加法器、二进制减法器和二进制除法之类的组合逻辑电路用于执行诸如乘法、加法、减法和除法之类的二进制算术运算。。。
在数字系统中,组合逻辑电路,如二进制乘法器、二进制加法器、二进制减法器和二进制除法,用于执行二进制算术运算,如两个二进制数字“0”和“1”的乘法、加法、减法和除法。这些被广泛用于各种应用,如计算机、手机、计算器、通用处理器和数字信号处理器,以通过各种算法处理信号。本文简要描述了二进制乘法器用于二进制乘法。
什么是二进制乘法器?
二进制乘法器的定义是:;执行两个二进制数(0和1)相乘的电子设备或数字设备或组合逻辑电路。二进制乘法中使用的两个二进制数或两个二进制输入是被乘数和乘法器,从而得到二进制乘积。
乘法器和被乘数的比特大小可以改变。但是二进制乘积的比特大小取决于乘法器和被乘数的比特大小。乘法器和被乘数的比特大小之和等于最终二进制乘积的比特大小。
二进制乘法器的功能
在二进制乘法器过程的第一步中,通过逐位乘法获得部分乘积项,这等于两个二进制数的“与”运算。在下一步中,将每列的所有部分乘积项相加,得到最终的二进制乘积输出。
该乘法器的逻辑电路设计随着比特大小而变化,并且其复杂性随着乘法器的比特大小的增加而增加。当要相乘的两个比特被馈送为具有不同比特大小的输入时,它由AND门函数控制。
该乘法器的主要功能是对2个不同比特大小的二进制数进行二进制乘法,并减少计算机等电子数字系统中的计算时间。二进制乘法与十进制乘法相似。
二进制乘法器的规则
与其他二进制运算一样,这种涉及二进制乘法的乘法器要容易得多,并且与十进制乘法相似。有乘数和被乘数。乘法的结果就是乘积。它只执行二进制数(0和1)的二进制乘法,所以您只需要将0和1相乘。以下是二进制乘法器对二进制乘法的规则。
规则1:0×0=0
根据这个规则,零的二进制乘积本身等于零。所以零和零的二进制乘积是零。
规则2:0×1=0
零和一的二进制乘积是零。
规则3:1×0=0
一和零的二进制乘积是零。
规则4:1×1=1(不适用结转或借入)
一和一的二进制乘积是一
真值表
这个二进制乘法器真值表如下所示。
| 输入A (乘数) |
输入B(乘法器) | 输出C (二进制产品) |
| 0 |
0 | 0 |
| 0 |
1. | 0 |
| 0 | 0 | 0 |
| 1. | 1. | 1. |
二进制乘法器类型
以下是二进制乘法器类型。
1) 2×2二进制乘法器或2位乘法器。
–使用2位全加法器的2位乘法器。
–使用单个单比特加法器的2位乘法器。
2) 3×3二进制乘法器或3位二进制乘法器。
–使用3位全加法器的3位二进制乘法器。
–使用单比特加法器的3位二进制乘法器。
3) 4×4二进制乘法器或4位乘法器。
–使用4位全加法器的4位二进制乘法器。
3×3二进制乘法器
3×3二进制乘法器是组合逻辑电路中的一种,它可以对两个比特大小最大为3比特的二进制数进行二进制乘法。所得到的输出二进制乘积的比特大小是6。
考虑被乘数A0 A1、A2和乘法器B0、B1、B2,以及作为P0、P1、P2输出的最终二进制乘积。这3个部分乘积项是在二进制乘法中获得的,因为它是一个3位乘法器。这种3×3乘法器可以使用3位全加法器和单独的单比特加法器来实现。考虑使用3位全加法器的3位乘法器的逻辑电路设计,如下图所示。
A2 A1 A0(被乘数)
X B2 B1 B0(乘法器)
——————————————
A2B0 A1B0 A0B0
A2B1 A1B1 A0B1 X
A2B2 A1B2 A0B2 X X X
———————————————
A2B2+C+C A2B2+A1B2+A2B2+C+C A1B1+C+A0B2+A2B0 A0B1+A1B0 A0B
当A2B0和A1B1相加在一起时,进位位被提升。通过将由此获得的和相加,从A0B1和A0B2到A1B0的相加获得进位位,这可以提高另一个进位位。因此,获得2个进位比特并将其进位以用于A2B1和A1B2的相加,并且以相同的方式生成另外2个进位位。
与其他方法相比,这种方法非常简单。该电路设计有3位全加法器,用于将3个部分乘积项相加。第一个部分乘积的最低有效位(LSB)不被添加到下一个部分乘积,因为它被作为所获得的最终二进制乘积输出的LSB。
根据上述逻辑电路,一个3位全加法器用于将前2个部分乘积相加在一起,另一个3比特全加法器将第三部分乘积与第一加法器的和相加。
电路设计所需的与门数量由公式m*n确定,其中“m”是乘法器位,“n”是被乘数位。所需加法器的数量由公式(m-1)确定,以产生m+n个比特。因此,这个3位乘法器需要9个与门和两个3位全加法器。
当三个部分乘积项相加在一起时,每个3位全加器的和的LSB直接作为输出,剩余的3位加到下一个部分乘积。
使用移位方法的二进制乘法器
作为并行二进制乘法器电路的替代方案,可以使用n位加法器、4个寄存器(a、B、C和Q)、偏移和控制逻辑来实现手动乘法方法,如下图所示。
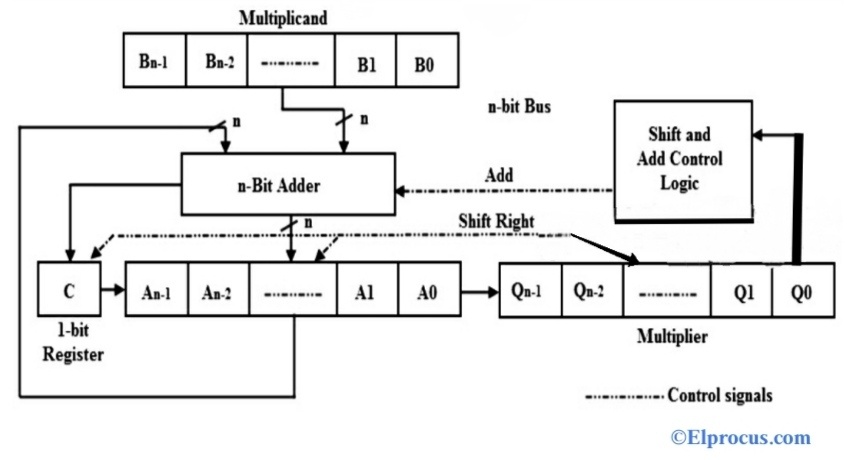
在这种方法中,4位乘法器被存储在Q寄存器中,4比特被乘数被存储在B寄存器中,并且A寄存器最初被设置为零。乘法过程从检查数字B的LSB(最低有效位)是0还是1开始。
如果B0=1,被乘数(B)中的数字与寄存器A的LSB相加,并且寄存器C、A和Q中的所有位都稍微向右移动一位。
如果位B0=0,则寄存器C和Q的组合向右移位一位,而不需要任何额外的处理。该过程对于n个比特重复n次。这种二进制乘法方法被称为使用移位法的并行乘法或使用移位方法的二进制乘法器。
考虑下图,其中乘法器和被乘数的值显示为1011和1101,它们分别加载到寄存器Q和A中。寄存器C最初被设置为0,因此寄存器A也是0,并且进位被另外存储。
由于B0=1,我们将B中的数字与A中的位相加,则相加结果为1101,并且Q和A寄存器向右移位1位,使得第一周期期间的新值为0110和1101。您必须重复此过程4次才能执行4位乘法运算。乘法的最终结果在寄存器A和Q中可用10001111,如图所示。
无符号4×4二进制乘法器采用两个4位输入,产生一个8位输出。类似地,8×8乘法器通过两个8位输入产生16位的输出。这种带有逻辑电路的乘法器是在具有各种引脚配置的集成电路(IC)上实现的,用于微处理器的多种应用,如控制设备、计算机、手机、计算器、DSP等。
使用ASM图表的二进制乘法器
二进制乘法器使用ASM图表(算法状态机)实现二进制乘法的算法,如下图所示。
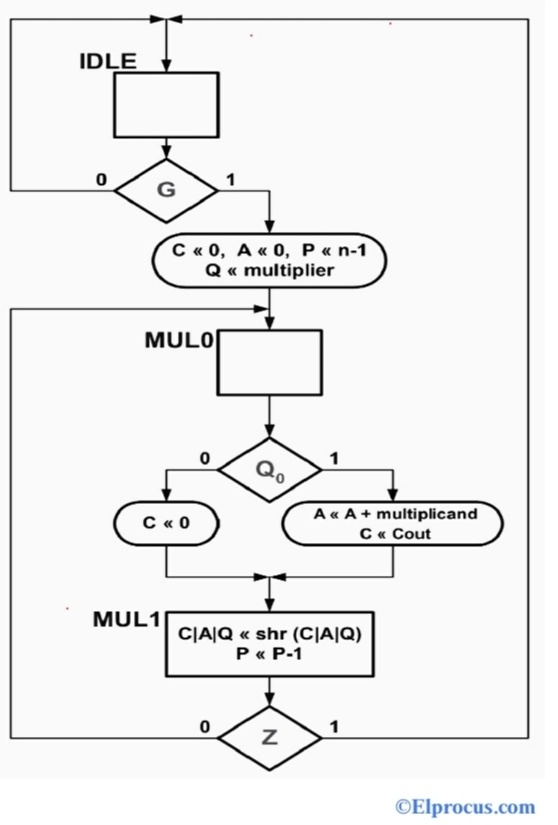
根据上述算法,“<<”被指示用于分配。例如,“C<<0”表示“C设置为0”。
在这个过程中,像IDLE、MUL0和MUL1这样的3个状态被用来向数据路径提供控制信号以执行乘法序列。该过程从“G”输入开始。只要G保持MUL0,ASM就会保持IDLE(空闲)状态。当G=1时,二进制乘法过程开始。当ASM移动到MUL0状态时,进位触发器和寄存器A被清除(C<<0和A<<0),计数器被预设为n-1(P<<n-1),Q寄存器被加载乘法器。
在MUL0状态下,乘法器的每个位的值(在Q0上可用)决定被乘数是否相加(Q0=1)(Q0=0)。如果Q0=0,则进位触发器被清除。如果Q0=1,则进位触发器存储从加法器获得的Cout(进位输出)。
在MUL1状态下,进位触发器、A寄存器和Q寄存器被表示为(1+n+n)位寄存器,并一起向右移动一个位置。在ASM图表中,这表示为C|A|Q<<shr(C|A| Q)。然后计数器也递减,这表示为(P<<P-1)。Z值确定,
- 返回MUL0状态(如果Z=0)以继续迭代或
- 返回IDLE(空闲)状态(如果Z=1)以完成该过程。注意,如果Z=1,则计数器从n-1向下计数到0,从而完成n次迭代。
如果状态IDLE=0,则乘数指示为“当前正在相乘”。如果IDLE=1(ASM图表返回IDLE=1),则表示二进制乘法过程已完成。
在设计过程的这一点上,控制信号被识别。这可以通过观察数据路径和ASM图表来完成。下面的表格显示了对数据路径中的每个组件进行的所有操作以及相应的控制信号名称。
| 数据路径组件 |
活动 | 控制信号Nam锿 |
| 进位触发器 |
C<<0,C<<Cout(来自加法器) | 清除_C 负载 |
| 计数器P |
P<<n-1和P<<P-1 | 初始化 班次(_D) |
| 寄存器A | A<<0 A<<A+乘数 C|A|Q<shr(C|A| Q) |
初始化 一条面包 班次(_D) |
| 寄存器Q | Q<<乘数 C|A|Q<shr(C|A| Q) |
初始化 班次(_D) |
二进制乘法器框图
二进制乘法的过程分为数据路径和控制逻辑/控制器两部分。下图显示了带有数据路径和控制逻辑的乘法器框图。
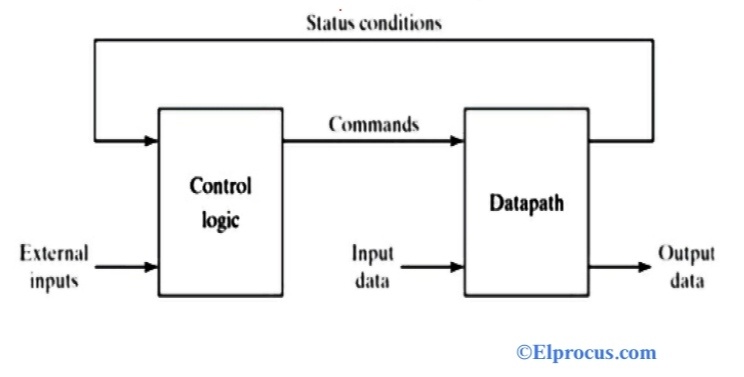
数据路径用于根据系统的要求操作数据。控制逻辑或控制单元或控制器用于生成用于对数据处理器中的操作进行排序的信号。
从上面的框图可以看出,
输入数据:被乘数(n位)和乘数(n位数)
输出数据:二进制乘积(2n位)
控制器或命令的控制信号:清除每个移位寄存器的进位、加载、移位和清除,并初始化(针对计数器)。
状态条件:Z(零检测)和Q0(乘法器的每个位)
二进制乘法器Verilog代码
让我们来看看数据流建模和行为建模中的2×2二进制乘法器Verilog代码。
数据流建模中的2×2二进制乘法器:
图书馆ieee;
使用ieee.std_logic_1164.all;
实体乘法是
端口(A,B:在bit_vector中(1向下到0);
P: out bit_vector(3到0)
);
结束乘法;
multiply is的体系结构数据流
开始
P(0)<=A(0)和B(0);
P(1)<=(A(1)和B(0))XOR(A(0)和B(1));
P(2)<=((A(1)和B(0))和(A(0)和B;
P(3)<=((A(1)和B(0))和(A(0)和B;
终端架构;
行为建模中的2×2二进制乘法器Verilog码
图书馆ieee;
使用ieee.std_logic_1164.all;
实体multiply_behav是
端口(A,B:在bit_vector中(1向下到0);
P: out bit_vector(3向下到0);
结束多重behav;
多功能behav的体系结构行为开始
过程(A,B)为
开始
情况A是
当“00”=>
如果B=“00”,则P<=“0000”;
否则,如果B=“01”,则P<=“0000”;
否则,如果B=“10”,则P<=“0000”;
否则P<=“0000”;
结束if;
当“01”=>
如果B=“00”,则P<=“0000”;
否则,如果B=“01”,则P<=“0001”;
否则,如果B=“10”,则P<=“0010”;
否则P<=“0011”;
结束if;
当“10”=>
如果B=“00”,则P<=“0000”;
否则,如果B=“01”,则P<=“0010”;
否则,如果B=“10”,则P<=“0100”;
否则P<=“0110”;
结束if;
当“11”=>
如果B=“00”,则P<=“0000”;
否则,如果B=“01”,则P<=“0011”;
否则,如果B=“10”,则P<=“0110”;
否则P<=“1001”;
结束if;
最终案例;
结束过程;
终端架构;
优势
这个二进制乘法器的优势如下所示。
- 中间乘积项或部分乘积项非常容易生成并且很简单。
- 它将被乘数与不同比特大小的乘法器相乘,并且它们的比特大小的范围可以变化。
- 它有助于减少用信号处理器中的算法处理数字信号所需的时间。
- 可用于小型集成电路,用于计算机、手机、计算器和处理器等商业电子应用。
- 与二进制加法器和二进制减法器相比,电路设计很简单。
- 成本较低。
应用
这个二进制乘法器的应用如下所示:
- 用于计算机。
- 用于手机。
- 用于高速计算器。
- 用于数字信号处理器。
- 用于控制设备。
- 用于数字通信系统。
1). VHDL中的二进制乘法器是什么?
该乘法器的VHDL程序可以用三种方式编写。他们是,
- 一种是数据流建模,它使用方程描述通过每个逻辑门的数据流。
- 行为建模通过使用顺序语句来定义实体的行为
- 结构建模借助于电路中各个部件的互连来描述电路。
2) 实现2位二进制乘法器需要什么?
2位二进制乘法器通过总共使用2个XOR门和6个and门来实现,或者可以使用4个and门和2个半加法器来实现。
因此,这一切都是关于在各种电子设备中使用的二进制乘法器的概述。在这里,二进制乘法器计算器用于非常快速和容易地执行2种二进制数字格式的二进制乘法,而无需使用手动方法。这里有一个问题,什么是ASM图表?
