超前进位加法器——电路、真值表和应用
不同类型的数字系统是由极少数类型的基本网络配置构建的,如与门、与非门、或门等。这些基本电路在各种拓扑组合中反复使用。。。。
不同类型的数字系统由极少数类型的基本网络配置构成,如与门、与非门、或门等。这些基本电路在各种拓扑组合中反复使用。除了执行逻辑外,数字系统还必须存储二进制数。对于这些存储器单元,也被称为FLIP-FLOP。执行一些功能,如二进制加法。因此,为了执行这些功能,在单片IC上设计逻辑门和FLIP FLOP的组合。这些集成电路构成了数字系统的实用构建块。用于二进制加法的构建块之一是进位先行加法器。
什么是超前进位加法器?
数字计算机必须包含能够执行加法、减法、乘法和除法等算术运算的电路。其中,加法和减法是基本运算,而乘法和除法分别是重复加法和减法。
为了执行这些操作,使用基本逻辑门来实现“加法器电路”。加法器电路发展为半加法器、全加法器、纹波进位加法器和进位超前加法器。
在这些超前进位加法器中,速度更快的是加法器电路。它通过使用更复杂的硬件电路来减少加法过程中出现的传播延迟。它是通过变换纹波进位加法器电路来设计的,使得加法器的进位逻辑变为两电平逻辑。
4位超前进位加法器
在并行加法器中,每个全加法器的进位输出被作为下一个高阶状态的进位输入。因此,这些加法器不可能产生任何状态的进位和求和输出,除非进位输入可用于该状态。
因此,为了进行计算,电路必须等待,直到进位位传播到所有状态。这导致电路中的进位传播延迟。
考虑上面的4位纹波进位加法器电路。这里,只要给出输入A3和B3,就可以产生和S3。但是在进位位C2被应用之前不能计算进位C3,而C2取决于C1。因此,为了产生最终的稳态结果,进位必须在所有状态中传播。这增加了电路的进位传播延迟。
加法器的传播延迟计算为“每个门的传播延迟乘以电路中的级数”。对于大量比特的计算,必须添加更多的级,这使得延迟更加糟糕。因此,为了解决这种情况,引入了超前进位加法器。
为了理解超前进位加法器的功能,下面介绍4位超前进位加法器。
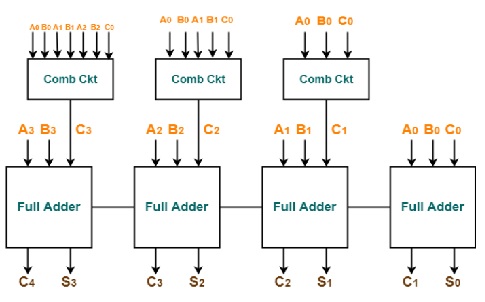
在该加法器中,加法器的任何级的进位输入与在独立级生成的进位位无关。这里,任何级的输出仅取决于在前一级中添加的比特和在开始级提供的进位输入。因此,在任何阶段的电路都不必等待来自前一阶段的进位位的生成,并且可以在任何时刻评估进位位。
超前进位加法器真值表
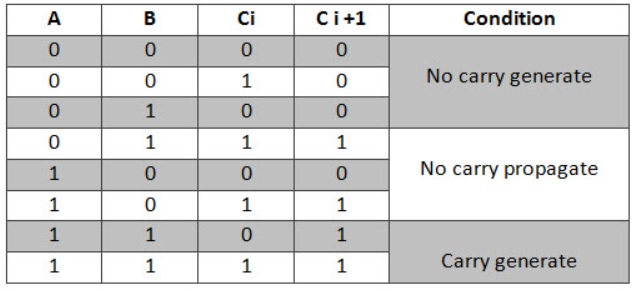
为了推导这个加法器的真值表,引入了两个新项——进位生成和进位传播。每当产生进位Ci+1时,进位产生Gi=1。这取决于Ai和Bi的输入。当Ai和Bi都为1时,Gi为1。因此,Gi被计算为Gi=Ai.Bi。
进位传播Pi与进位从Ci到Ci+1的传播相关联。它被计算为Pi=AiŞBi。这个加法器的真值表可以从修改全加法器的真数值表中导出。
使用Gi和Pi项,求和Si和进位Ci+1如下所示——
- Si=πŞGi。
- Ci+1=Ci.Pi+Gi。
因此,进位比特C1、C2、C3和C4可以计算为
- C1=C0.P0+G0。
- C2=C1.P1+G1=(C0.P0+G0).P1+G1。
- C3=C2.P2+G2=(C1.P1+G1).P2+G2。
- C4=C3。P3+G3=C0.P0.P1.P2.P3+P3.P2.P1.G0+P3.P2.G1+G2.P3+G3。
从等式中可以观察到,进位Ci+1仅取决于进位C0,而不取决于中间进位位。
电路图
上述方程是使用两级组合电路以及AND、OR门来实现的,其中假设门具有多个输入。
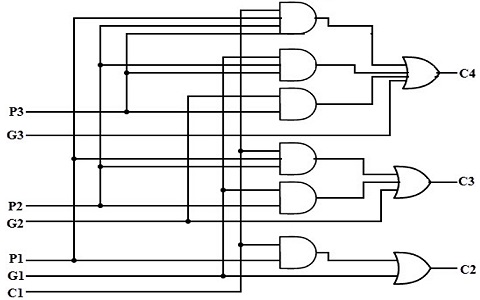
下面给出了4位的超前进位加法器电路。
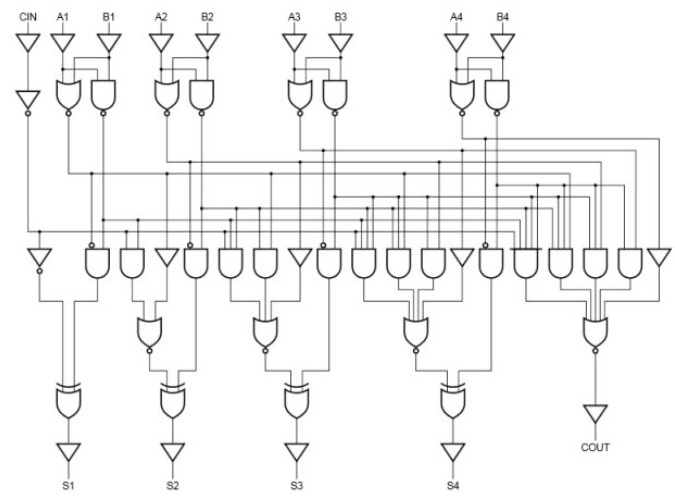
8位和16位进位先行加法器电路可以通过将4位加法器电路与进位逻辑级联来设计。
超前进位加法器的优点
在该加法器中,减少了传播延迟。任何阶段的进位输出仅取决于起始阶段的初始进位位。使用这个加法器可以计算中间结果。这个加法器是用于计算的最快的加法器。
应用
高速超前进位加法器被用作实现为IC的加法器。因此,很容易将加法器嵌入电路中。通过组合两个或多个加法器,可以很容易地进行高位布尔函数的计算。这里,当用于较高的比特时,门的数量的增加也是适度的。
对于这个加法器,在面积和速度之间有一个折衷。当用于高位计算时,它提供了高速,但电路的复杂性也增加了,从而增加了电路所占的面积。该加法器通常被实现为4位模块,当用于更高的计算时,这些模块被级联在一起。与其他加法器相比,这种加法器的成本更高。
对于计算机中的布尔计算,加法器被定期使用。Charles Babbage在计算机中实现了一种预测进位位的机制,以减少由纹波进位加法器引起的延迟。在设计系统时,计算速度是设计者的最高决定因素。1957年,Gerald B.Rosenberger为现代二进制进位超前加法器申请了专利。基于对门延迟的分析和仿真,正在进行实验以修改该加法器的电路,使其更快。对于n位进位超前加法器,当给定每个门的延迟为20时,传播延迟是多少?
图片来源
研究大门
