乘法器用于广泛的数字信号处理和其他应用中。由于当前技术的进步，许多研究人员主要关注设计因素，以获得更好的性能。一些设计目标是——高速、准确、低功耗、布局规则、面积更小。DSP处理器有各种计算块，如多路复用器、加法器、MAC。与以前的版本相比，这些块的操作和执行速度有所提高。乘法器的执行速度取决于两个因素，半导体技术和乘法器架构。加法器是数字多路复用器的基本组成部分，我们在其中执行一系列重复加法，为了加快乘法器的运算速度，必须提高加法器的运算速度。有许多数字信号处理应用，其中关键的延迟路径和处理器的性能取决于乘法器。乘法器有多种类型，其中4×4阵列乘法器是本文介绍的一种先进乘法器。


4×4阵列乘法器中的乘法方案

乘法方案有两种

串行乘法（Shift–Add）：串行乘法运算可以通过找到部分乘积，然后将部分乘积相加来解决。实现是原始的，具有简单的体系结构

并行乘法：并行乘积是在并行乘法和高性能机器中同时生成的。应用并行实现，将延迟降至最低。

乘法算法

乘法过程有三个主要步骤：

  • 部分产品生成
  • 部分产品减少
  • 最后添加。

常见的乘法方法是“加法和移位”算法。N位乘法器的乘法算法如下所示。

ding="async" class="size-full wp-image-37565" src="https://uploads.9icnet.com/images/aritcle/20230518/4-by-4-multiplication.jpg" alt="4-by-4-multiplication" width="475" height="413" sizes="(max-width: 475px) 100vw, 475px">
4乘4乘

 

4 - by - 4 - multiplication 1
4–乘–4–乘法1
example-2
示例-2

部分乘积使用AND门生成，其中

  • 被乘数=N位
  • 乘法器=M位
  • 部分乘积=N*M。

两个8位数字的乘积，生成16位乘积。

加法方程式为

P（m+n）=A（m）。B（n）=i=0 m-1∑j=0n-1∑ai bj 2i+j……。1.

A、 B＝8比特；

乘法中的步骤

以下是任何乘法运算的步骤

  • 如果乘法器的LSB为“1”。然后将被乘数加到累加器中，乘数位向右移动一位并且被乘数位向左移动一位。
  • 当乘法器的所有位都为零时停止。
  • 如果部分产品是串行添加的，则使用较少的硬件。我们可以通过并行乘法器将所有PP相加。然而，可以使用压缩技术，在进行添加之前可以减少部分产物的数量。

不同类型的乘法器

不同类型的乘法器是，

展位乘数

布斯乘法器的功能是，将2个以2的补码形式表示的有符号二进制数相乘。布斯乘法器的优点是最小复数，可以加快乘法运算。展位乘数的缺点是功耗高。

组合乘法器

组合乘法器对两个无符号二进制数进行乘法运算。组合乘法器的优点是它可以很容易地生成中间乘积。组合乘法器的主要缺点是它占据了很大的面积。

顺序乘法器

乘法被划分为一系列步骤，其中生成的部分乘积被添加到累加器，现在部分和被转移到下一步。这样做的优点是占地面积较小。顺序乘法器的缺点是它是一个缓慢的过程。

Wallace树乘法器

它减少了部分乘积的数量，并使用进位选择加法器对部分乘积进行加法运算。Wallace树乘法器的优点是具有高速和中等复杂度的设计。Wallace树乘法器的主要缺点是布局设计不规则，占地面积较大。

阵列乘法器

乘法器电路基于加法-移位算法。阵列乘法器的主要优点是设计简单，形状规则。阵列乘法器的缺点是延迟高并且功耗高。

移位和加法乘法器

它类似于我们在数学中所做的普通乘法过程，来自数组乘法器流聊天，其中X=乘法；Y=乘数；A=累加器，Q=商。首先检查Q是否为1或否，如果为1，则将A和B相加并将A_Q算术右移，否则如果不是1，则直接将A_Q运算右移并将N递减1，在下一步骤中检查N是否为0或否。如果N不是0，则从Q＝0重复步骤，否则终止过程。

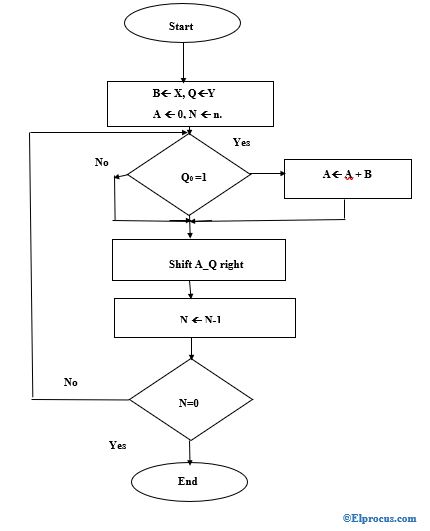
shift-and-add-multiplier
移位和加法乘法器

4×4阵列乘法器的构造与工作

阵列乘法器的设计结构是规则的，它是基于加移位算法的原理。

部分乘积=被乘数*乘数位………。(2)

在AND门用于乘积的情况下，使用全加法器和半加法器进行求和，其中部分乘积根据它们的位阶进行移位。在n*n阵列乘法器中，n*n个与门计算部分乘积，部分乘积的加法可以通过使用n*（n–2）个全加法器和n个半加法器来执行。所示的4×4阵列乘法器有8个输入和8个输出

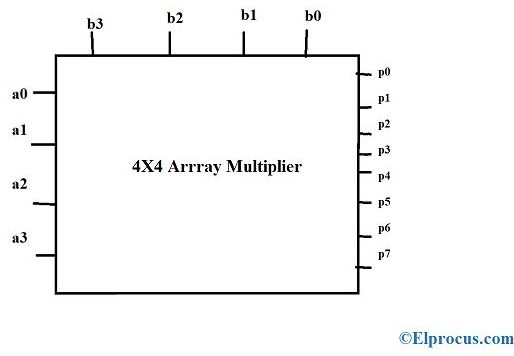
4-by-4-array-multiplier
4乘4阵列乘法器

4×4阵列乘法器的构建块

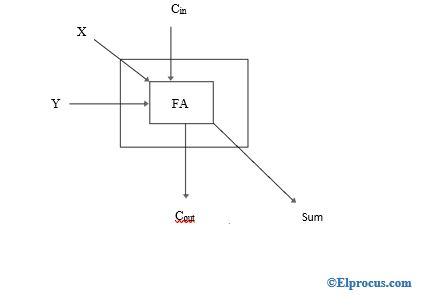
全加法器有三条输入线和两条输出线，我们将其用作阵列乘法器的基本构建块。以下是4×4阵列乘法器的示例。最左边的比特是部分乘积的LSB比特。

adder-block-diagram
加法器方框图
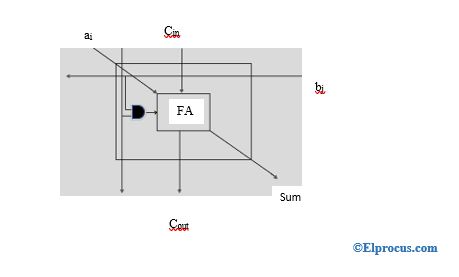
array-multiplier-block-diagram
阵列乘法器框图

最右边的位是部分乘积的MSB位。现在，在乘法运算中，部分乘积向左侧移动，然后将它们相加，得到最终乘积。重复此过程，直到没有两个部分产物退出以进行添加。

4-by-4-multiplication-1
4乘4乘1
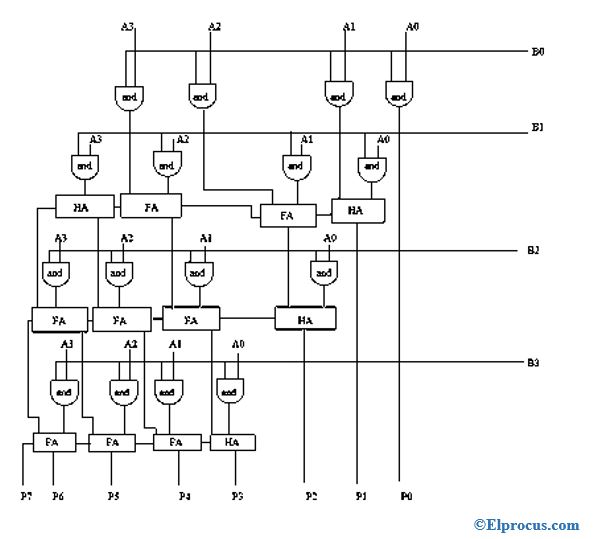
logic-diagram-of-4-by-4 - array - multiplier
4乘4的逻辑图–阵列–乘法器

其中a0，a1，a2，a3和b0，b1，b2，b3是被乘数和乘数，所有乘积的总和是偏积。偏积总和的结果是乘积。

对于4×4阵列乘法器，它需要16个与门、4个半加法器（HA）和8个全加法器（FA）。总共12个加法器。

4×4阵列乘法器的优点

阵列乘法器的优点是，

  • 最低复杂度
  • 易于扩展
  • 易于管道化
  • 形状规则，易于放置和布线

4×4阵列乘法器的缺点

阵列乘法器的缺点如下，

  • 高功耗
  • 更多的数字门导致大面积。

4×4阵列乘法器的应用

列举了阵列乘法器的应用，

  • 阵列乘法器用于执行算术运算，如滤波、傅立叶变换、图像编码。
  • 高速运行。

因此，这一切都是关于4×4阵列乘法器，这是一种基于加法和移位原理的高级乘法器，使用结构简单的流水线技术可以很容易地提高性能，尽管它使用了更多的逻辑门，可以使用Verilog来实现。这里有一个问题，“设计3*3阵列乘法器需要多少逻辑门？”。