在电子领域，我们经常听到交流和直流这两个术语。因此，交流波形就是与交流电流相关的波形。这意味着它是一种在负值和正值之间切换的周期性波形。用来表示这一点的最常见的波形类型是正弦波形。当达到直流波形时，电流和电压值基本处于稳定状态。它被如此简化以表示稳定值及其幅值。但根据上面的讨论，AC波形的幅度值并不是那么简单，因为它对应于时间连续变化。要知道这一点，有很多方法，最流行的方法是“RMS电压”。本文清楚地解释了整个均方根电压理论、方程、适用方法和其他内容。


什么是RMS电压？

定义：首先，将其扩展为均方根值。许多人对此给出的一般定义是计算出的AC功率的量，该AC功率提供与DC功率对应的相同量的加热功率，但RMS电压具有额外的功能。它被称为瞬时生成值的二重函数的平均值的√。

该值表示为V<sub>均方根值RMS电流值为I均方根值.

ding="async" class="size-medium wp-image-39604" src="https://uploads.9icnet.com/images/aritcle/20230518/RMS-Voltage-Waveform-300x188.png" alt="RMS Voltage Waveform" width="300" height="188" sizes="(max-width: 300px) 100vw, 300px">
RMS电压波形

RMS值仅针对波动时间的正弦电压或电流值计算，其中波的幅度对应于时间而改变，但不用于计算DC波形值，因为幅度保持恒定。通过将提供类似电量的AC正弦波的RMS值与作为类似DC电路的所提供负载进行比较，则该值被称为有效值。

这里，有效电流值表示为I有效有效电压值为V有效或者，有效值也被表示为DC波的多少安培或伏特与产生类似量的功率的能力相类似。

方程式

更重要的是要了解RMS电压方程其中它被用来计算许多值，并且基本方程是

五、均方根值=伏峰值电压*（1/（√2））=V峰值电压* 0.7071

RMS电压值基于AC波幅度值，并且它不依赖于交流波形的相位角或频率。

例如：当交流波形的峰值电压为30伏时，RMS电压计算如下：

五、均方根值=伏峰值电压* (1/ (√2)) = 30 * 0.7071 = 21.213

结果值在图形和分析方法中几乎相同。只有在正弦波的情况下才会发生这种情况。而在非正弦波中，图解法是唯一的选择。不使用峰值电压，我们可以使用存在于两个峰值之间的电压来计算，即VP型.

这个正弦RMS值计算如下：

五、均方根值=伏峰值电压*（1/（√2））=V峰值电压* 0.7071

五、均方根值=伏峰值电压*（1/2（√2））=V峰值* 0.3536

五、均方根值=伏平均的* (∏/（√2）=V平均的* 1.11

RMS等效电压

主要存在两种用于计算正弦波或甚至另一复杂波形的RMS电压值的通用方法。方法是

  • 均方根电压图解法–用于计算随时间变化的非正弦波的RMS电压。这可以通过指向波浪中的纵坐标来实现。
  • 均方根电压分析方法–用于通过数学计算来计算波的电压。

图形化方法

该方法显示了计算波的正半部分和负半部分的RMS值的相同过程。因此，本文解释了正循环的过程。该值可以通过考虑整个波形上类似间隔的瞬间的特定精度来计算。

正半周期被分成“n”个相等的部分，也被称为中间坐标。当有更多的中间坐标时，结果会更准确。因此，每个中间纵坐标的宽度都是n度，高度是波浪在x轴上的瞬时值。

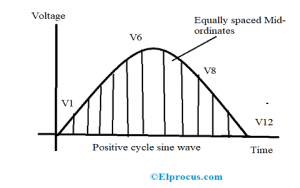
Graphical Method
图解法

这里，波浪中的每个中间纵坐标值都会加倍，然后添加到下一个值。这种方法提供了RMS电压的平方值。然后，将获得的值除以中间纵坐标的总数，得到RMS电压的平均值。因此，RMS电压方程由下式给出

Vrms=[中间坐标的总和×（电压）2]/中间坐标的数量

在以下示例中，有12个中间纵坐标，RMS电压显示为

五、均方根值=√（V1.2.+五2.2.+五3.2.+五4.2.+五5.2.+五6.2.+……+V122.)/12

让我们考虑交流电压的峰值电压为20伏，考虑到10个中间纵坐标值，其给出如下

五、均方根值= √(6.22.+ 11.82.+ 16.22.+ 192.+ 202.+ 16.22.+ 11.82.+ 6.22.+ 02.)/10 = √(2000)/12

五、均方根值=14.14伏

图形方法在知道正弦或对称的交流波的RMS值方面显示出极好的结果。这意味着图形方法甚至适用于复杂的波形。

分析方法

在这里，这种方法只处理正弦波，通过数学方法很容易找到RMS电压值。一种周期性的正弦波是恒定的，并且给出为

五、（吨）=伏最大值*cos（ωt）。

在这种情况下，正弦电压V的RMS值（吨）是

五、均方根值=√（1/T）T0五、最大值2.*科斯2.（ωt））

当积分极限考虑在0之间时0和3600然后

五、均方根值=√（1/T）T0五、最大值2.*科斯2.（ωt））

总的来说，对应于AC电压，RMS电压是最好的表示方式，其中它表示信号幅度、电流和电压值。RMS值与整个瞬时值的中值不相似。与RMS电压和峰值电压值的比例等于RMS电流和峰值电流值。

许多万用表设备——电流表或电压表——在考虑精确正弦波的情况下计算RMS值。为了测量非正弦波的RMS值，“精确万用表”是必要的。通过正弦波的RMS方法找到的值提供了与DC波类似的加热效果。

例如，我2.R=I均方根值2.R。在交流电压和电流的情况下，如果不将它们视为其他值，则必须将其视为RMS值。因此，10安培的交流电将提供与10安培的直流电类似的加热效果，峰值约为14.12安培。

因此，这一切都是关于RMS电压的概念、其方程、正弦波形、用于计算这些电压值的方法，以及详细的均方根电压理论此外，了解如何通过RMS计算器将峰值电压、平均电压和峰间电压转换为RMS电压吗？